现在的位置:主页 > 期刊导读 >
Matlab在圆形断面特征水深计算中的应用_
【作者】网站采编【关键词】【摘要】1 引言 水力计算中经常会遇到圆形断面正常水深、临界水深和收缩水深的求解问题,其实质是求解含参变量的非线性方程或超越方程,此类方程没有求根公式,不能直接计算,传统的计
1 引言
水力计算中经常会遇到圆形断面正常水深、临界水深和收缩水深的求解问题,其实质是求解含参变量的非线性方程或超越方程,此类方程没有求根公式,不能直接计算,传统的计算方法主要有:①试算法,即利用试探法与二分法进行试算,计算繁杂,工作量大;②图表法,即利用已经制好的大量图表求解,由于此类图表种类多,使用麻烦,而且精度欠佳。
近十多年来,国内外专家学者针对圆形断面特征水深的计算问题,进行了大量研究,他们的研究成果主要集中在两个方面:①引入无量纲水深,通过对特征水深方程的数学变换,得到无量纲水深的近似直接计算公式[1~9];②采用逐次逼近原理进行迭代计算,通过选取合适的迭代初值和迭代方程计算特征水深[10~12];另外,也有部分专家学者采用其它方法计算特征水深,如殷彦平等[13]将圆形断面正常水深问题转化为非线性约束优化问题,应用混合模式搜索法求解水深;张新燕等[14]利用非线性函数模型,通过Marquardt 法建立了正常水深的直接计算公式。另外,这些研究成果大部分都集中在圆形断面的临界水深和正常水深的计算中,对于圆形断面收缩水深的计算研究较少。
非线性代数方程的求解大部分都可以通过数学软件来实现,Matlab 以其强大的编程及计算功能而被广泛地应用于求解非线性代数方程中。
Matlab 是集数值分析与计算、微积分与矩阵运算、工程与科学绘图、数字图像处理、数字信号处理、语言编程于一体的一款工程软件。Matlab 操作简单,易于掌握。文中采用Matlab 中查找函数零点的命令fzero 及语言编程,对圆形断面临界水深、正常水深和缩水深进行编程计算,其程序简洁明了,易于操作,而且效率和精度都非常高。
处在那样的年纪,未来还没有被定义,生活冉冉升起。大家每天雄赳赳气昂昂,开始买日本的电器看美国的电影。拿到爱华随身听,激动得整晚睡不着觉,翻来覆去听张学友。香港是怎样的,让人神往。
2 用Matlab 求解圆形断面特征水深
2.1 圆形断面临界水深的计算
2.1.1 圆形断面临界水深的求解公式
水力学中临界流的基本方程为:
如图1 所示,圆形断面的水力要素分别为:
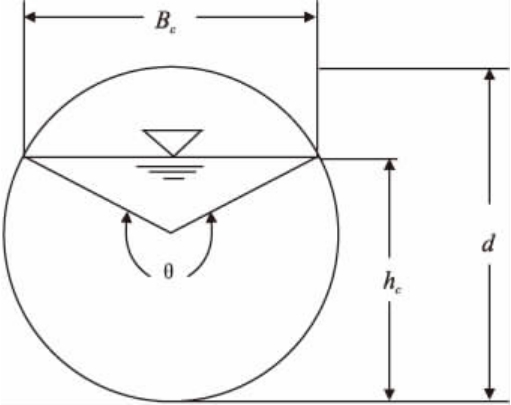
图1 圆形过水断面
过水断面面积:
水面宽度:
>>alpha=1.0;
式中:Q 为过水流量,m3/s;Ac 为临界流对应的过水断面面积,m2;Bc 为水面宽,m;g 为重力加速度,通常取9.81 m3/s;a 为流速分布不均匀系数,通常取1.0;θ 为临界水深对应的圆心角,rad;d 为圆形断面直径,m。
将式(2)、式(3)代入式(1)得:
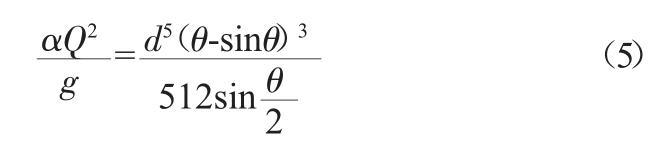
将上式变形得:
William Bernard Jones用两个话题说明己方政策的确存在着一定的缺陷,即在经过漫长的独裁统治后,叙利亚的重建一定会是一个漫长而且昂贵的过程。但是,他又通过另外一个话题说明土耳其不会孤军奋战,己方期望阿拉伯联盟,伊斯兰合作组织和欧盟会成为土耳其的合作成员。

由此可见:式(6)为关于θ 的含参数的超越方程,理论上无解析解。因此可以利用Matlab 编程求出θ,然后代入式(4)可求出临界水深hc。
2.1.2 工程实例
以文献[3]为例,某圆形断面的引水式电站输水隧洞,洞径d=15.0 m,求设计流量Q=1 m3/s 时的临界水深。
利用Matlab 求解圆形断面临界水深程序如下:
在Matlab 语言中:alpha 表示α,theta 表示θ.
>>syms alpha Q g d theta
临界水深:
要形成良好的创业生态,需要具备一定的条件,这些条件可以是国家政策的倾斜、科研院校的集中,也可以是本地区悠久的创业文化、传统的优势产业。经过30多年的发展,东营市经济发生了很大变化,逐渐摆脱了对油田的依赖,并形成了自己的优势产业,石油化工及盐化工、橡胶轮胎及汽车零部件、有色金属、石油装备等在全国具有一定知名度,这些优势产业既是东营市经济发展的支柱产业,也是东营市吸引创业者的优质名片。但从东营市目前出台的创业扶持政策看,多是实行普惠制,很少专项惠及这些产业。本地优势创业项目得不到有力支持,这对于东营市的创业吸引力是非常不利的。
>>Q=1;
综上,通过技术经济比较,对于±800 kV滇西北至广东特高压直流输电工程共塔架设段线路,推荐采用提高接地极线绝缘配置的反事故措施,将由操作过电压水平确定的9片170 mm结构高度绝缘子提高到由雷电过电压水平确定的15片170 mm结构高度绝缘子。
>>g=9.81;
①过水断面面积,计算见式(2)。
>>f=@ (theta)(512*alpha*Q^2*sin (theta/2)./(g*d^5)).^(1/3)-theta+sin(theta);
>>theta=fzero(f,[0.000001 2*pi])
theta=0.5440
>>hc=1/2*d*(1-cos(theta/2))
2.2.1 圆形断面正常水深的求解公式
即临界水深hc=0.2757。
用孙建公式、王正中公式和赵延风公式分别计算本例,结果见表1。
表1 临界水深不同计算公式误差比较

公式名称 临界水深(m) 临界水深精确解(m) 相对误差(%)孙建公式[1] 0.2754 0.2757 -0.112王正中公式[2] 0.2661 0.2757 -3.493赵延风公式[3] 0.2755 0.2757 -0.070本文公式 0.2757 0.2757 0.000
2.2 圆形断面正常水深的计算
hc=0.2757
水力学中圆形断面均匀流方程为:

上式两边同时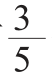 次幂,得到:
次幂,得到:

圆形断面的水力要素为:
1)采用改进的Gibson公式得到了双壁厚及等壁厚类方形蜂窝夹芯结构的等效弹性参数,发现这2种不同壁厚类方形蜂窝夹芯的面外刚度、yoz面等效剪切模量及等效密度等有较大差异,这为进一步研究类蜂窝夹层板的振动特性奠定了基础。
①过水断面面积,根据式(2)计算。
顾客信任指顾客对他与员工之间建立起一种可靠和诚信关系的自信[24]。本文采用Roberts等[43]的测量量表,根据服务情境对表述进行调整,包括正直(honesty)和善意(benevolence)两方面,共6个测量项目。如“这位销售人员对产品和服务中存在的问题是诚实的”(正直),“这位销售人员关注我的利益”(善意)。
近年来,随着高校基础设施的完善和投入的持续增加,我国高校场馆设施逐步增多,开放率有较大提高。“六普”统计数据显示,2013年高等院校体育场地对外开放情况为:不开放场馆设施数为27 393个,占比55.06%;部分时段开放10 294个,占比20.69%;全天开放场馆设施数为12 063个,占比24.25%[7]。有将近一半左右的高校在满足日常体育教学需要的同时,选择对外开放场馆设施,为公众参与体育活动提供了较多高品质的健身场所,有效缓解了公众健身场地设施不足的困境,而高校场馆设施对外开放只是迈出了场馆高校利用的第一步,在未来还应继续探索多元化运营模式。
②湿周:
那时的我们,不经世事,无关风月。这份纯粹与美好,在以后的三十年里,再也没有出现过。后来,我们天各一方,杳无音讯。时间,也就永远地定格在了十五六岁的年纪。至于再见,以及再见之后的种种,其实是为了真正意义上的结束,再也找不回当初的模样了。但至今我仍然非常努力,想要葆有一颗初心,一份纯真,尽管世事多艰,人心难测。而我,仍在这繁华都市的街头,寻找曾经路过的自己,或者你,或者我们。
③正常水深:
式中:n 为粗糟系数;Q 为过水流量,m3/s;i 为底坡;Ac 为发生均匀流时的过水面积,m2;Bc 为水面宽度,m;p 为湿周;hc 为均匀流水深,m;d 为圆形断面直径,m;θ 发生均匀流时的圆心角,rad。
将式(2)、式(9)代入式(8)中得:
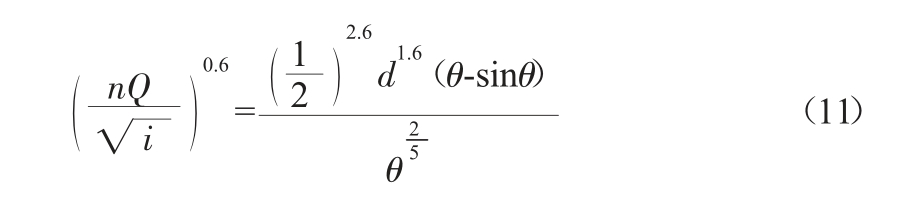
将上式变形得:
由此可见,式(16)为关于θ 的含参数的超越方程,理论上无解析解。因此可以利用Matlab 编程求出θ,然后代入式(14)可求出收缩水深.
2.2.2 工程实例
伽达默尔的哲学诠释学并非是一种方法论,而是一种本体论的诠释学。应用在这里绝不是理解的一种方法,通过运用此种方法才可以达到理解。上文所考察的各种理解的实际情况,其目的也并非是对理解做一种方法论上的启示,提示大家该如何去做才能获得理解(虽然会有此种效果),而仅仅是描述理解现象本身。在文本的理解和解释之中已然包含了对于该文本的应用,而对该文本的应用就是对此文本的理解和解释。
以文献[7]为例,某圆形断面的引水式电站输水隧洞,已知断面底坡,i=0.001 粗糟系数n=0.015,洞径d=15.0 m,求设计流量Q=840 m3/s 时的正常水深。利用Matlab 求解圆形断面正常水深程序如下:
在Matlab 语言中:theta 表示θ,i 表示虚数单位,所以i 用I 表示,以示区别。
>>syms n Q I d theta
>>hk=1/2*d*(1-cos(theta/2))
脱了衣服,竹韵才发觉刚才的热水已经给龙斌洗澡用完了,于是,她干脆扭开自来水龙头用凉水冲起来。水虽然有点凉,但还能适应,她边洗边想,下个月领了工资,首先得买台热水器,免得天天要烧水。
>>Q=840;
>>I=0.001;
>>d=15;
>>f=@ (theta)(2^2.6* (n*Q/sqrt(I))^0.6*theta^0.4./d^1.6)-theta+
sin(theta);
>>theta=fzero(f,[0.000001 2*pi])
theta=4.2640
>>n=0.015;
hk=11.4915
即正常水深hk=11.4915。
用文献[1]和文献[2]中的公式分别计算本例,结果见表2。
表2 正常水深不同计算公式误差比较
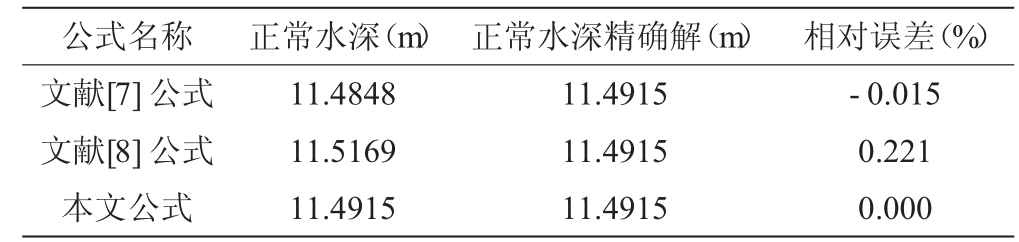
公式名称 正常水深(m) 正常水深精确解(m) 相对误差(%)文献[7]公式 11.4848 11.4915 -0.015文献[8]公式 11.5169 11.4915 0.221本文公式 11.4915 11.4915 0.000
2.3 圆形断面收缩水深的计算
2.3.1 圆形断面收缩水深的求解公式
发动机没有能量是不会自行转动的,肌肉没有能量就不会收缩,人也就无法运动。我们的一日三餐实际上就是人体能量的来源,食物经过消化、吸收,其中有一部分转化为葡萄糖贮藏在肌细胞里。
水力学中圆形断面收缩流的方程为:
圆形断面的水力要素为:
>>d=15;
②收缩水深:
式中:E0 为上游断面总水头,m;Q 为过水流量,m3/s;hs 为收缩水深,m;d 为圆形断面直径,m;φ为流速系数;θ 发生收缩流时的圆心角,rad。
将式(2)、式(14)代入式(13)中得:
将上式变形得:
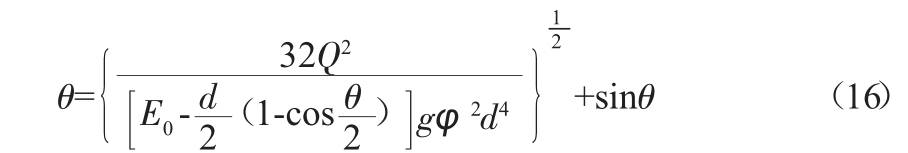
求出θ 后,代入式(14)可求出收缩水深。
由此可见,式(12)为关于θ 的含参数的超越方程,理论上无解析解。因此可以利用Matlab 编程求出θ,然后代入式(10)可求出正常水深hk。
2.3.2 工程实例
以文献[9]为例,已知坝(闸)前断面总水头E0=12 m,圆形断面直径d=15.0 m,流速系数φ=0.95,求设计流量Q=500 m3/s 时的收缩水深。
利用Matlab 求解圆形断面临界水深程序如下:
在Matlab 语言中:phi 表示φ,theta 表示θ。
>>syms phi Q g d theta E0
>>g=9.81;
>>phi=0.95;
在目前的法律体制下,进一步细化和明确公益诉讼制度的职责主要在司法机关。但是,考虑到司法机关对推动某一具体行政管理领域的公益诉讼制度建设缺乏积极性,而其他行政部门往往只关注其职能范围内的公益诉讼制度建设,因此,作为水资源统一监督和管理部门,水行政主管部门应当在推动水资源保护公益诉讼制度建设中扮演更加积极的角色。一方面,要加强与司法机关的沟通,积极推动“两高”在司法解释或指导性案例中纳入水资源保护公益诉讼;另一方面,要积极与立法部门及相关行政部门沟通联系,在相关法律修改(如将来可能开展的《水法》修改)中纳入水资源保护公益诉讼的内容。
>>Q=200;
>>d=15;
就他本人研究初唐诗而言,章句家的诗、类书家的诗和“诗中的诗”,均有眼力判断。他的《孟浩然》是从孙润夫家藏的王维所画的“孟浩然像”说起,《贾岛》开篇勾勒贾岛、姚合阴黯的形象,确乎源自性格的考量。定其品第,别其体性,估其价值,用历史的眼光来研究,则已然是“综合”下一阶段的重心了。
>>E0=12;
>>f=@ (theta) (32*Q^2./ ((E0-d* (1-cos (theta/2))./2)*g*phi^2*d^4))^(1/2)-theta+sin(theta);
>>theta=fzero(f,[0.000001 4.39])
theta=1.5367
>>hs=0.5*d*(1-cos(theta/2))
hs=2.1071
即收缩水深hs=2.1071。用赵延风公式计算本例,结果见表3。
表3 收缩水深不同计算公式误差比较

公式名称 收缩水深 收缩水深精确解 相对误差(%)赵延风公式 2.104 2.107 -0.138本文公式 2.107 2.107 0.000
3 结论
从表1、表2 和表3 的误差比较可以看出,应用Matlab 数学软件求解的圆形断面的正常水深、临界水深和收缩水深,不仅程序简单明了,而且计算精度高,方法更容易掌握。Matlab 作为一种强大的工程软件,必将会广泛应用在水力计算和水利设计中。
[1]孙建,李宇.圆形和U 形断面明渠临界水深直接计算公式[J].陕西水力发电,1996,12(3):38-41.
[2]王正中,陈涛,万斌,等.圆形断面临界水深的新近似计算公式[J].长江科学院院报,2004,21(2):1-2,9.
[3]赵延风,何晓军,祝晗英,等.无压流圆形断面临界水深的新近似计算公式[J].人民长江,2009,40(11):76-79.
[4]王正中,冷畅俭,娄宗科.圆管均匀流水力计算近似公式[J].给水排水,1997,(9):27-29.
[5]韩会玲,孟庆芝.非满流圆管均匀流水力计算的近似数值解法[J].给水排水,1994,(10):25-26.
[6]文辉,李风玲,黄寿生.圆管明渠均匀流的新近似计算公式[J].人民黄河,2006,28(2):67-68.
[7]赵延风,祝晗英,王正中.一种新的圆形过水断面正常水深近似计算公式[J].河海大学学报:自然科学版,2010,38(1):68-71.
[8]赵延风,芦琴,张宽地.圆形过水断面均匀流水深的近似计算公式[J].西北农林科技大学学报:自然科学版,2008,36(5):225-228.
[9]赵延风,王正中,孟秦倩.无压流圆形断面收缩水深的近似计算公式[J].水利水电科技进展,2009,31(2):6-8.
[10]吕宏兴,把多铎,宋松柏.无压流圆形过水断面水力计算的迭代法[J].长江科学院院报,2003,20(5):15-17.
[11]张宽地,吕宏兴,赵延风.明流条件下圆形隧洞正常水深直接计算法[J].农业工程学报,2009,25(3):1-5.
[12]邹武停,辛全才.基于牛顿迭代法的圆形断面临界水深的直接计算[J].水电能源科学,2012,(03):100-102.
[13]殷彦平,吕宏兴,张宽地.求解圆形排水管道正常水深的一种新方法[J].水利与建筑工程学报,2011,(04):18-21.
Application of Matlab in the Calculation of Water Depth of the Circular Section
文章来源:《陕西水利》 网址: http://www.sxslzz.cn/qikandaodu/2020/0522/353.html

